Secciones:

Novedades

Un paper del arXiv

En un rincón de la red

Problem(it)a

---

Novedades

UMA

Septiembre. Pasó la reunión anual de la UMA, realizada con la Sociedad Matemática de Chile, a la cual no asistí, y me perdí la charla de Maria Victoria Otero Espinar sobre competición entre lenguajes.

Este es uno de mis temas favoritos, al que vuelvo una y otra vez. Empecé de casualidad hace muchos años, cuando alguien me llamó la atención sobre un artículo que había sido mencionado en distintos diarios de todo el mundo. El artículo, de Abrams y Strogatz, había aparecido en Nature: Modelling the dynamics of language death. Me preguntó si se lo podía conseguir, y con ese título fue imposible que no lo leyera.

Con el tiempo, descubrí los trabajos de Daniel Nettle, y luego los de otros antropólogos, más los mapas de Ethnologue (por ejemplo, exploren los de Nigeria, Indonesia o Papúa-Nueva Guinea, países con más de 500 lenguajes en cada uno).

Hay una gran comunidad estudiando el problema de la extinción de lenguajes, a la que se han sumado físicos y matemáticos. Se utilizan diferentes tipos de modelos: simulaciones con agentes, modelos como los del votante o el de Axelrod, ecuaciones diferenciales ordinarias y en derivadas parciales, etc. Los modelos de agentes (discretos) y los de campo medio (continuos) capturan ciertos aspectos del problema, y algunos de estos aspectos son más fáciles de estudiar con unos, pero intratables con los otros.

* * * Luego, María Victoria dio una charla en el Departamento de Matemática, FCEN, UBA. Hablé del crecimiento de la carrera de Matemática (y las vinculadas, títulos mixtos con computación y física), que están entre las más solicitadas en España. Un dato interesante es que en Madrid la nota de corte para el ingreso fue la más alta, superando a Medicina. También detallé las vinculaciones con industrias, educación media y la divulgación, que llevaron a la población de matemáticos a una tasa de desempleo que es menor que la mitad de la tasa general de España.

---

Un paper del arXiv

Voy a comentar rápido un paper que esté en el arXiv desde el año pasado, A fractal proof of the infinitude of primes, de Kota Saito.

Como la demostración es muy sencilla, voy a desarrollarla casi por completo. En realidad, sólo necesitamos una definición y un par de lemas.

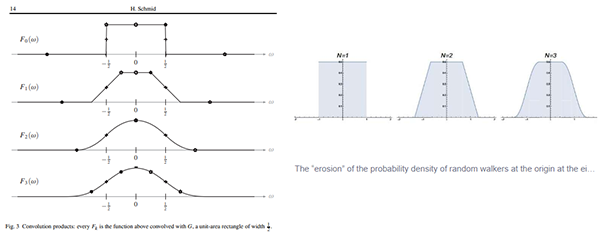
Definición: Dado C en la recta, su dimensión Box, DB(C) se define como un límite cuando d tiende a cero,

DB(C) = lim -log(N(d))/log(d),

donde N(d) es el mínimo número de intervalos de longitud d que necesito para cubrir C.



Lema 1: Si A y B son conjuntos en la recta, y AB es el conjunto de todos los productos entre los elementos de A y de B, entonces

DB(AB) es menor o igual que DB(A) + DB(C).



Lema 2: Si A es el conjunto de números (1/n) con n natural, DB(A)=1/2.

El Lema 1 se puede ver en cualquier libro clásico: Falconer, Mattila, etc. La demostración del 2 es un ejercicio sencillo, una cuenta parecida a la que sigue:



Lema 3: Si Pp es el conjunto de todas las potencias naturales de un primo p, digamos (1/p^k), entonces DB(Pp)=0.

Demostración: Tomemos d=1/p^n para un n fijo. Ahora, con n intervalos cubrimos seguro Pp, porque podemos usar el [0,d], y luego, como mucho, uno para cada uno de los n-1 números restantes.

Calculemos log(N(d)) y log(d):

log(N(d)) = log(N(1/p^n)) = log(n)

log(d) = log(1/p^n)) = n log(1/p)

Y listo, porque log(n)/n tiende a cero.

Ahora sí, el teorema:

Teorema: Existen infinitos números primos.

Demostración: Supongamos que fueran finitos, p,..., q. Como cada número es producto de potencias de éstos,

A = Pp ... Pq

Pero entonces

1/2 = DB(A) < DB(Pp) ... DB(Pq) = 0

. Tremendo!

---

En un rincón de la red

Visto en Facebook

La profesora Hartkopf dictando su curso "Fracciones: cómo enfrentarse a ellas y resolver todos los problemas#.
* * *

Solo en twitter

Via Alessandro Vespignani:



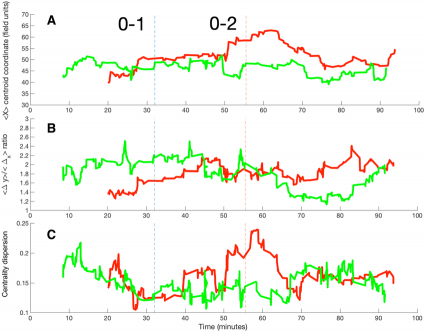
En el trabajo estudian la red de pases entre los jugadores. El paper completo se puede ver (gratis) aquí, Scientific Reports 9 13602 (2019).

Personalmente, la evoluci�n de los parámetros de la red a lo largo de un partido crítico me parece lo mejor:

---

Un problem(it)a

7.- Biyección: Tenemos una función f del (1, ..., n) en sí mismo, biyectiva. ¿Es cierto que para algún N se tiene que componer f N veces es la identidad? Es decir, f(f(...(i))...) = i para todo i entre 1 y n?

* * *

Solución del mes anterior

6.- Pescadores: Nicolás con su hijo, y Pedro con su hijo, fueron a pescar. Nicolás pescó tantos como su hijo. Pedro pescó el triple que su hijo. Entre todos, trajeron 35 pescados.

¿Cómo se llama el hijo de Pedro?

Solución: Si el hijo de Nicolás pescó x, y el hijo de Pedro pescó y, en total pescaron

x+x+y+3y = 2x + 4y = 2(x+2y)
Como es una cantidad par, nunca puede ser 35.

Pero observemos que no leímos la pregunta... Con los datos que nos dan, qué pasaría si Nicolás fuera el hijo de Pedro: ahora el hijo de Nicolás pescó x, Nicolás también pescó x, y Pedro pescó 3x, con lo cual

x+x+3x = 5x = 35 y encontramos x=7.

Es decir, el hijo de Pedro se llama Nicolás.

* * *
¿Soluciones? ¿Otras soluciones? ¿Variantes? ¿Errores? ¿Comentarios? ¿Preguntas? Me encuentran en jpinasco@gmail.com.