Secciones:

Novedades

Un paper del arXiv

En un rincón de la red

Problem(it)a

---

Novedades

(I)

Agosto parecía un mes tranquilo, donde no pasaba gran cosa, pero terminó con un escándalo en la comunidad matemática uruguaya al que es difícil no refererise y hacer como que "acá no ha pasado nada". Las denuncias de acoso (laboral, sexual), las cartas cruzadas a favor y en contra de los implicados, los testimonios de diferentes actores (autoridades, docentes, alumnos), muestran una situación muy compleja parcialmente basada en una mal entendida horizontalidad. Les recomiendo los tweets de Jana Rodriguez Hertz al respecto aquí @janarhertz.

* * *

(II)

Por otra parte, Steven Strogatz en el New York Times, al igual que cientos de columnas de noticias, tweets, blogs, y demás elementos de la fauna digital, discutían si 8 / 2 (2+2) es igual a 1 � a 16.

Kenneth Chang, también en el New York Times lo plantea muy bien: Why Mathematicians Hate That Viral Equation? It's formatted to confuse people, and there are no interesting underlying concepts.

Mucho más entretenido fue este otro meme que también circuló en relación al anterior (coincido, actually funny rather than stupid, como dice @kj_cheetam):



* * *

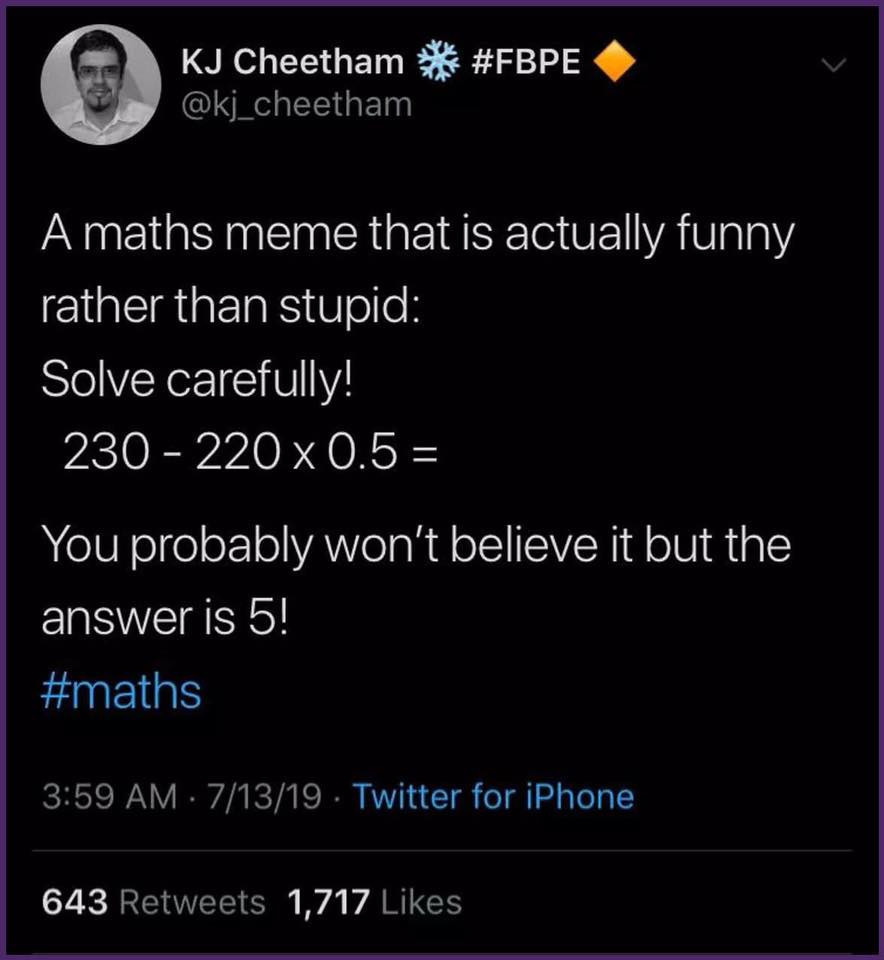
(III)

A fines de agosto se realizó el Festival Matemático 4D en el CCK, organizado por el Departamento de Matemática de Exactas, UBA, el Area de Matemática del CBC, UBA, y Moebius, Imaginación a las aulas.

Se encuentran ya en youtube algunas de las actividades del festival, se accede clickeando en el 4D verde del video:

---

Un paper del arXiv

En esta ocasión quería hablar del trabajo When random walkers help solving intriguing integrals, de S.N. Majumdar y E. Trizac, publicado ahora en Phys. Rev. Lett. 123 (2019).

O, para ser preciso, quería hablar de los comentarios que aparecieron al respecto en Physics Today y en Phys Org en julio y agosto.

Prehistoria: A principios de siglo (de este, el XXI), David y Jonathan Borwein publicaron Some remarkable properties of sinc and related integrals, donde estudiaron unas integrales hoy llamadas Borwein integrals. Si uno agrega términos escalando la variable por un impar, sigue dando pi/2 hasta que llegamos al 15 y falla por menos de 10^(-10). Una imagen es más clara:

The Borwein integral: why pattern generalization sometimes can go wrong pic.twitter.com/zXN23NL0WM

� Fermat’s Library (@fermatslibrary) October 22, 2017

Physics Today: El artículo de Hill afirma que el trabajo de Majumdar y Trizac había sido inspirado por el tweet anterior, pero no pude encontrar ninguna refencia al respecto en el mismo, ni en la intro ni en las notas de la bibliografía. Una verdadera pena si realmente fue así.

Inmediatamente después afirma:

Although mathematicians found an expression for when the result changes, they lack an intuitive understanding why. To fill that gap, Majumdar and Trizac have offered a way to visualize the behavior of Borwein integrals using one-dimensional random walkers.

Luego, sigue una descripción muy clara del contenido del paper.

Phys Org: El artículo Illusive patterns in math explained by ideas in physics de Zyga arranca ya desde el título con una exageración, y continúa con un comentario como el anterior:

[T]wo physicists have approached these integrals using the physics concept of random walks. Whereas solving these integrals usually requires a great deal of effort and ingenuity, the physicists have shown that the new approach can find solutions intuitively and sometimes even without the need for explicit calculations.

pero va aún más lejos al afirmar:

Although the theorem helps to explain when the Borwein integrals' temporary patterns break, it is still not completely clear why the theorem holds in the first place.

In the new paper, Majumdar and Trizac have offered some physical intuition into the theorem by connecting it to some well-understood concepts in probability theory and statistical mechanics. They noticed that the integral in the theorem has close ties to the uniform probability distribution, which is widely used throughout science. Specifically, the Fourier transform of the uniform probability distribution happens to be just the sinc function, which yields the Borwein integral for n = 1.

�Y los Borwein no se dieron cuenta...

...de que sinc era la transformada de Fourier de una uniforme?

...de la interpretación probabilística?

...de la relación con los paseos al azar?

Bueno... de hecho se dieron cuenta: la transformada aparece en la primera página, y tras demostrar el teorema, introducen la interpretación probabilística en el punto (ii) del Remark 1 de su trabajo, donde escriben explícitamente una suma de uniformes sorteadas en [-1,1] y cada paso escalado por el factor correspondiente! (página 8 en el pdf linkeado antes).

Además, la idea de que la convolución y la transformada erosionan la característica del intervalo [-1,1] fue utilizada por Schmid en Two curious integrals and a graphic proof, Elemente der Matematik 2014, con gráficos muy claros de qué está pasando.



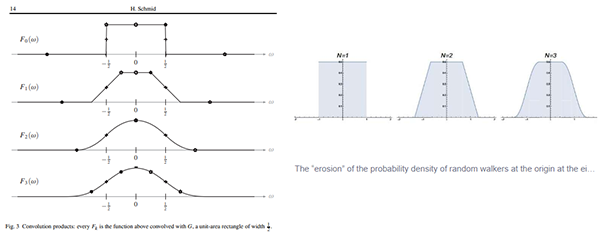
¿Entonces?

Volviendo al paper de Majumdar y Trizac, si bien por momentos parecen no ser conscientes de que esta idea ya estaba en el trabajo original (sí del uso de la transformada), realizan un aporte muy interesante. Tras describir el argurmento, extienden este tipo de integrales (y el fenómeno de transición de fase cuando un parámetro cruza cierto umbral) a funciones más generales: distintas clases de funciones de Bessel, funciones hipergeométricas, y a problemas en dimensiones superiores, entre otras cosas.

Nada que reprocharles a ellos, en todo caso, a los divulgadores que no se tomaron el trabajo de chequear exactamente quién hizo cada cosa.

* * *
Una parte divertida de la historia:

Cuando los Borwein calcularon estas integrales por primera vez vieron que en la octava no daba pi/2, pero el error era muy pequeño, menor a 10^(-10). Las probaron en el software de cálculo Maple, que las calculó correctamente, pero igual se comunicaron con la gente de Maple y les dijeron que había algo raro con el programa. La pobre persona encargada de buscar el error pasó tres días trabajando hasta que sospechó que le estaban haciendo una broma. El mismo confirma la historia en los comentarios a un post de MathOverflow, aquí.

---

En un rincón de la red

Visto en Facebook

De Hadoopy memes.
* * *

Solo en twitter

Bruce Willis: Hay cuatro elementos, ¿verdad?
Productor: Adelante...
Bruce Willis: ¿qué tal si hubiera un QUINTO elemento?
Productor: Me encanta!
Bruce Willis: Ok, y viste que hay cinco sentidos...
...
[horas después]
...
Bruce Willis: hay muchos, muchos boy scouts...
Productor: ... [llora]...
Bruce Willis: ¿qué tal el ULTIMO boy scout?


Basado en el tweet de @ItsAndyRyan y los comentarios. Es interesante la cantidad de referencias numéricas en los títulos de las películas de Bruce Willis: 10 Minutes Gone, Catch .44, Dos inútiles en patrulla, 7 el número equivocado, Entre dos fuegos, 12 monos, Cuatro habitaciones, The First Deadly Sin.

---

Un problem(it)a

6.- Pescadores: Nicolás con su hijo, y Pedro con su hijo, fueron a pescar. Nicolás pescó tantos como su hijo. Pedro pescó el triple que su hijo. Entre todos, trajeron 35 pescados.

¿Cómo se llama el hijo de Pedro?

* * *

Solución del mes anterior

5.- Digitos al azar: repartimos los números del 1 al 9 al azar en una grilla de 3x3. ¿Cuál es la probabilidad de que las sumas de los dígitos de cada una de las filas y en cada una de las columnas sea siempre impar?

¿Y si reparto los números del 0 al 8? Solución: empecemos observando que como nos interesa la paridad de las sumas, no importa si ponemos los números 1, 2,..., 9 o simplemente cinco unos y cuatro ceros (correspondientes al 1, 3, 5, 7, y 9; y al 2, 4, 6, y 8, respectivamente).

Como queremos que la suma de cada fila y cada columna sea impar, necesitamos que en una misma fila (y columna) haya dos ceros o ninguno, así que tenemos que seleccionar en qué par de filas ubicamos los ceros, y dentro de estas dos filas, en qué dos columnas estarán. Esto es el combinatorio de 3 tomados de a 2 al cuadrado.

Ahora, todas las formas posibles de ubicar ceros en los 9 lugares es 9 tomados de a 4, con lo cual el cociente de casos favorables sobre casos posibles es

3 . 3 /(9 . 8 . 7 . 6 . 5/5 . 4 . 3 . 2) = 1 / (7 . 2) = 1/14

Para la segunda parte, la respuesta es cero! Ahora sólo tengo 4 números impares, y como cada fila/columna debería tener un número impar de unos, coloco un 1 en cada fila, pero el restante repite fila... y la suma de esa fila será par.

* * *
¿Soluciones? ¿Otras soluciones? ¿Variantes? ¿Errores? ¿Comentarios? ¿Preguntas? Me encuentran en jpinasco@gmail.com.