Gestión de aguas superficiales
Ir al artículo
Contaminación del agua
Ir al artículo
Ir al artículo
Ir al artículo
EVOLUCION EN LOS CRITERIOS HIDROLÓGICOS E HIDRÁULICOS DE LOS ALIVIADEROS PARA EL CONTROL DE CRECIDAS EN ARGENTINA
Rafael Santiago SEOANE (1,2,*) y Raúl Antonio LOPARDO (1,3)
(1) Instituto Nacional del Agua.
(2) Facultad de Ingeniería de la Universidad de Buenos Aires. Consejo Nacional de Investigaciones Científicas y Técnicas.
(3) Facultad de Ingeniería de la Universidad de la Plata.
INA, Casilla Correo 46 - (1802)-Aeropuerto Ezeiza, Buenos Aires, Argentina.
Palabras clave: modelos matemáticos, hidrología, hidráulica, crecidas, aliviadero, presiones fluctuantes.
Keywords: mathematical models, hydrology, hydraulics, flood, spillway, pressure fluctuations.
RESUMEN
La mayoría de las obras hidráulicas argentinas, fueron diseñadas y construidas con anterioridad al desarrollo de las teorías hidrológicas modernas, que permiten evaluar con cierto grado de certeza una adecuada "crecida de diseño". De forma similar, las nuevas tecnologías que permiten determinar los fenómenos hidráulicos que ponen en riesgo las obras de descarga, se han desarrollado también posteriormente, tomando en algunos casos la experiencia de las fallas observadas en las obras construidas. Las nuevas investigaciones en hidrología, que han utilizando la información de caudales extremos observados en distintos lugares del mundo, han demostrado la importancia de las características del clima sobre la variabilidad observada en las crecidas y la necesidad de estudiar la incertidumbre en las estimaciones de los caudales de diseño. A ese respecto, el trabajo pretende demostrar la importancia de avanzar en el desarrollo de estudios hidrológicos y en la investigación de las relaciones entre el clima y la ocurrencia de valores de caudales extremos. Ello permitirá estimaciones más precisas, revisar las obras cuyos parámetros fueron determinados con modelos obsoletos y también incorporar los nuevos datos hidrológicos observados ante las evidencias de un posible impacto del cambio climático global sobre los caudales extremos. Se demuestra la necesidad de adaptar los aliviaderos existentes para hacer frente a crecidas más exigentes, en virtud de cálculos hidrológicos más precisos y asimismo a los posibles efectos del cambio climático, para que las obras de disipación puedan hacer frente a esas nuevas condiciones, sin daños que comprometan la seguridad total de las obras. Ello requerirá, sin dudas, efectuar una nueva verificación experimental de las condiciones de funcionamiento de las estructuras sometidas a esfuerzos fluctuantes, cuyos valores extremos podrán ser modificados sensiblemente ante nuevas estimaciones de los caudales que deberán ser erogados por estructuras ya existentes.
1. INTRODUCCIÓN
Las obras hidráulicas se diseñan y construyen para aprovechar, con diversos propósitos, las corrientes de los cursos de agua y deben necesariamente disponer de estructuras que permitan evacuar los caudales excedentes en las mejores condiciones posibles.
Desde un punto de vista hidráulico, el aliviadero es fundamentalmente responsable de asegurar que el pasaje de las crecidas no produzca el sobrepaso de la obra de retención, con lo que se transforma en el elemento de seguridad de todas las estructuras componentes. El diseño de los aliviaderos depende directamente de la estimación de parámetros que son definidos aplicando modelos hidrológicos e hidráulicos de distinta complejidad.
El análisis de las obras construidas en la Argentina muestra que existen importantes embalses y obras hidráulicas realizadas desde principios del siglo XX. Sin embargo, los avances en la modelación matemática de los principales procesos hidrológicos e hidráulicos involucrados en la estimación de los parámetros fueron sólo muy significativos a partir de la década de los cincuenta del siglo pasado.
El objetivo de este trabajo es mostrar la importancia de la evolución de los criterios hidrológicos e hidráulicos aplicados en las estimaciones de los parámetros de diseño de las obras construidas en la Argentina durante el siglo XX.
Los resultados de este análisis demuestran la necesidad de realizar estudios de revisión y verificación de importantes obras hidráulicas construidas debido a que existen nuevos modelos y técnicas y un conjunto de observaciones hidrológicas y meteorológicas modernas disponibles.
2. PRESAS DE EMBALSE Y OBRAS HIDRÁULICAS EN LA ARGENTINA
Para mostrar la importancia del tema se realizó un análisis de la cantidad de obras hidráulicas y de los volúmenes de los embalses construidos durante el siglo XX. Se calcularon ambos indicadores para identificar los períodos de mayor actividad en la construcción y vincular la época de realización de la obra con los resultados del análisis histórico de la evolución de las teorías científicas.
Este análisis muestra la importancia de estudiar los avances en las técnicas de estimación de los parámetros de diseño de las obras hidráulicas y en la necesidad de incorporar la nueva información hidrológica observada desde la construcción, dado el tiempo transcurrido.
La ocurrencia de nuevos eventos de precipitación-caudal observados después de la finalización de las obras define la necesidad de la verificación de las crecidas de diseño de obras importantes para obtener una nueva estimación de los parámetros hidráulicos de sus aliviaderos y obras de control.
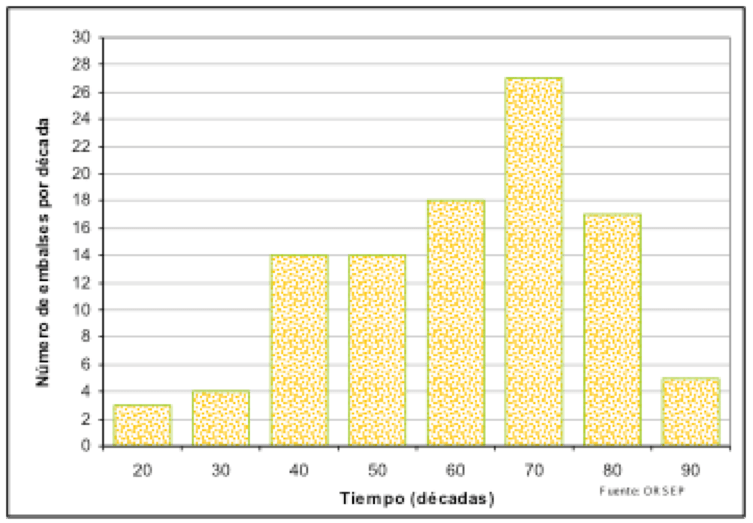
Figura N°1 Cantidad total de embalses construidos entre 1920 y 1990.
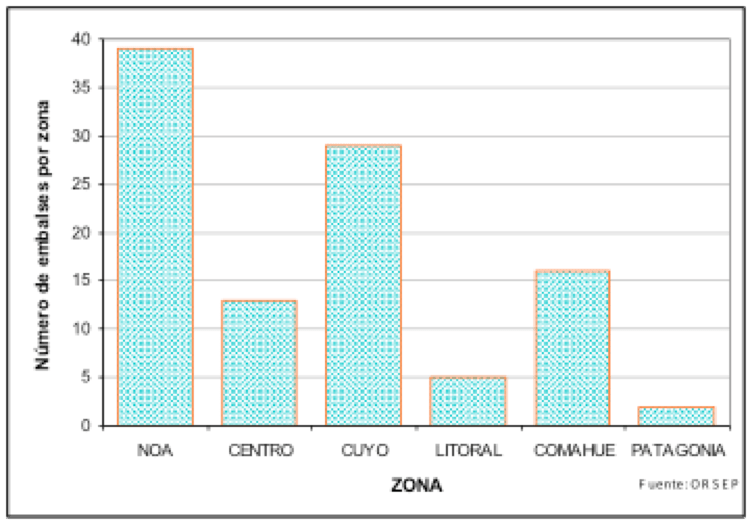
Figura N° 2 Número de embalses indicando las regiones climáticas.
En la figura Nº 1 se presenta la cantidad de las presas construidas entre los años 1920-1990, y se observa un máximo durante la década de los setenta. La figura Nº2 presenta la cantidad de las obras realizadas en ese período indicando los distintos climas de nuestro país y se muestra la significativa cantidad ubicadas en zonas áridas y semiáridas donde resulta necesario mejorar el aprovechamiento temporal del recurso agua.
En la Tabla Nº 1 se presentan algunos ejemplos de obras hidráulicas y se indica la región y la zona climática según la clasificación propuesta por Moyano y Díaz (2006).
La importancia de este análisis se relaciona con los resultados de actuales investigaciones en Hidrología que demuestran que existe una mayor incertidumbre para las estimaciones de los caudales máximos anuales en las regiones áridas y semiáridas que en las regiones húmedas ubicadas en distintas regiones del mundo (Meigh et al., 1997).
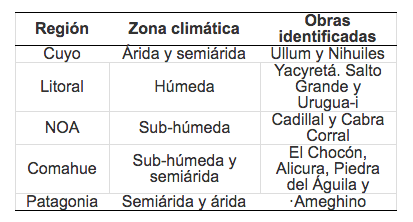
Tabla N° 1 Obras hidráulicas seleccionadas por zonas climáticas de la Argentina.
Los resultados presentados son consistentes con los estudios hidrológicos que indican que la Argentina es un país con dos tercios de su superficie con clima árido o semiárido y la mayor cantidad de su población se encuentra ubicada en las zonas de mayor disponibilidad hídrica.
En las otras regiones se observa la necesidad de mejorar la disponibilidad del recurso agua que ha llevado a la construcción de numerosos embalses en las zonas áridas y semiáridas.
Un ejemplo de este tema se presenta más adelante con un análisis de la evolución de los modelos de estimación de parámetros de los embalses construidos sobre los ríos Limay y Neuquén. Estos embalses reciben los aportes de las altas precipitaciones que ocurren en la Cordillera de los Andes y regulan el caudal con propósitos de control de crecientes, hidroelectricidad y riego.
3. ANÁLISIS DE LA PRESENCIA DE CAMBIOS EN TEORÍAS CIENTÍFICAS
En este parágrafo se presenta un enfoque basado en la idea más teórica de definir la presencia de cambios en los modelos explicativos que se utilizan para resolver problemas de Ingeniería. Por lo tanto, se ha seleccionado para el análisis de los cambios observados un modelo de transformación precipitación-caudal que mejora la precisión de las estimaciones de los caudales de diseño. Este modelo matemático tiene como objetivo relacionar las precipitaciones observadas con los caudales registrados a la salida de una cuenca hidrológica.
Una cuenca es definida como el área de drenaje cuya agua contribuye a un punto particular a lo largo de una red de canales (o una depresión) basada en su topografía superficial. La cuenca forma un elemento del paisaje (a varias escalas) que integra todos los aspectos del ciclo hidrológico dentro de un área definida que puede ser estudiada y cuantificada.
La selección del caudal como una variable hidrológica significativa se fundamenta en que es la variable que integra todos los procesos hidrológicos que ocurren en una cuenca y define su respuesta hidrológica. En la cuenca se estima el caudal total que presenta dos componentes: el caudal base, relacionado con el escurrimiento del agua subterránea, y el caudal directo asociado con el escurrimiento que se desplaza sobre la superficie del suelo.
Una teoría central para explicar la transformación precipitación-caudal ya presentada es el modelo del hidrograma unitario instantáneo. El modelo de hidrograma unitario instantáneo está configurado por una expresión matemática que relaciona las precipitaciones efectivas (precipitación total menos las pérdidas en el suelo debidas a la infiltración) con el caudal directo.
Desde un punto de vista histórico la teoría del hidrograma unitario comienza con versiones determinísticas: Sherman (1932), Snyder (1938), Clark (1945) y Nash (1957); luego las versiones desarrolladas a principios de los años 80 incorporan modelos probabilísticos en las explicaciones.
En consecuencia se propone la aplicación de una clasificación de modelos estadísticos para indicar la importancia de los cambios observados entre las distintas versiones de la teoría del hidrograma unitario (HU). Para comprender esto resulta conveniente describir la forma clásica de explicación científica denominada nomológica deductiva. Esta explicación está definida por un explanans, lo que explica, formado por leyes generales y enunciados con condiciones iniciales y un explanandum, lo que debe ser explicado, que contiene una descripción del fenómeno empírico a ser explicado, Shuster (1982).
En Hempel (1988) se indican algunas de las principales propiedades de las explicaciones deductivo-estadísticas al señalar que: "las explicaciones de este tipo serán llamadas deductivo?estadísticas o explicaciones D?E. Supone la deducción de un enunciado con la forma de una ley estadística a partir de un explanans que contiene indispensablemente por lo menos una ley o principio teórico de forma estadística. Se realiza la deducción por medio de la teoría matemática de la probabilidad estadística, que permite calcular ciertas probabilidades derivadas (las aludidas en el explanandum) sobre la base de otras probabilidades (especificadas en el explanans) halladas empíricamente o afirmadas hipotéticamente".
Los conceptos anteriores fundamentan la idea de que la versión propuesta por Rodríguez?Iturbe et al.(1982) es del tipo denominado deductivo-estadístico. En el nuevo modelo se aplican distintas leyes probabilísticas para deducir las funciones de densidad de probabilidades de las variables aleatorias caudal y tiempo al máximo del hidrograma unitario instantáneo geomorfoclimático. Entre las principales leyes probabilísticas utilizadas se incluyen las funciones de densidad de probabilidades exponenciales para representar la precipitación puntual (Rodríguez?Iturbe et al., 1982). Una descripción de la función de las leyes estadísticas aparece ya en Rodríguez-Iturbe y Valdés (1979), cuando proponen el hidrograma unitario instantáneo geomorfológico y señalan que Lienhard en el año 1964 proporcionó un enfoque puramente mecánico estadístico para el hidrograma unitario instantáneo.
Otras versiones de la teoría del hidrograma unitario instantáneo muestran distintas aplicaciones del modelo deductivo-estadístico y un caso interesante fue presentado por Rosso (1984) donde se relaciona los parámetros del modelo de Nash (1957) con el hidrograma unitario instantáneo geomorfológico de Rodríguez-Iturbe y Valdés (1979).
Otro trabajo importante para la estimación de caudales en cuencas con datos escasos es la propuesta de Wilson y Brown (1992). Estos autores desarrollan una nueva versión del hidrograma de Clark (1945) que considera como una variable aleatoria al coeficiente de almacenamiento adimensional del modelo y estudian su estimación con las funciones de densidad de probabilidades de Gumbel y Log-Pearson III.
La Tabla Nº 2 muestra la importancia de los cambios observados en las distintas versiones del hidrograma unitario instantáneo. Las versiones determinísticas de la teoría están asociadas con el modelo explicativo nomológico-deductivo y las estadísticas con el modelo deductivo-estadístico propuesto en la clasificación de Hempel.
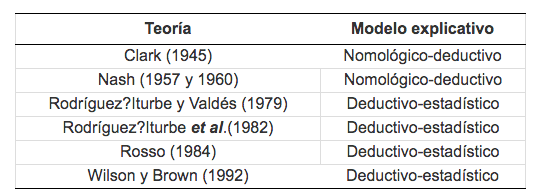
Tabla Nº 2. Modelos explicativos en la teoría del hidrograma unitario instantáneo.
Los conceptos desarrollados bajo diferentes modelos explicativos definieron la necesidad de verificar las obras dado el avance demostrado en las teorías.
Además, se puede afirmar que las obras hidráulicas construidas a principios del siglo XX se diseñaron utilizando los datos hidrológicos e hidrometeorológicos disponibles. En esa época la crecida de diseño de un vertedero obtenida con modelos estadísticos, que definen la relación caudal máximo-periodo de retorno, presentaba extrapolaciones considerables dada la escasa longitud de los registros de precipitación y caudal.
4. MODELOS HIDROLÓGICOS Y LA ESTIMACIÓN DE CAUDALES
Una alternativa metodológica para la estimación de los parámetros de un aliviadero consiste en estimar la relación caudal máximo-período de retorno. Las estimaciones de los caudales de diseño se obtienen ajustando una función de densidad de probabilidades a la serie de caudales máximos observados en una sección del curso de agua.
En el período entre los años de 1910 y 1930 se desarrollaron fórmulas empíricas para el análisis de frecuencia de los caudales máximos. Las expresiones permitían estimar los caudales máximos, para un dado periodo de retorno (cantidad promedio de años necesarios para que la variable aleatoria sea igualada o superada), utilizando la media de los caudales máximos diarios. Un ejemplo de esta metodología fue definida con datos observados en distintas cuencas de los Estados Unidos (Fuller,1914).
Además de aplicar el modelo de Sherman (1932), en la década de los años 30, se comenzaron a utilizar conceptos de meteorología para estimar los valores de la precipitación con la finalidad de mejorar el diseño hidrológico. Se utilizó por primera vez el concepto de un límite superior para la precipitación denominada precipitación máxima posible. Este término se utilizó en la mayoría de las publicaciones anteriores a 1950 referidas a la determinación de precipitaciones extremas.
Posteriormente, en la década de los 70, se reconoció que la transposición de tormentas observadas no podría conducir al límite superior de la precipitación en una cuenca. La precipitación asociada con los límites superiores es conocida actualmente como precipitación máxima probable (PMP) y se define como la mayor cantidad de precipitación meteorológicamente posible, correspondiente a una determinada duración, sobre un área de tormenta dada, en una ubicación geográfica particular y en determinada época del año, sin tener en cuenta las tendencias climáticas de largo plazo.
Los valores de PMP estimados bajo estas condiciones deberían actualizarse a medida que se avanza en el conocimiento de los procesos atmosféricos y se incorpora nueva información. Además, se debe agregar un modelo de transformación precipitación-caudal como la teoría del hidrograma unitario instantáneo cuya evolución se discute más adelante.
La Crecida Máxima Probable (CMP) se define como la crecida que puede ser esperada a partir de las más severas combinaciones críticas de las condiciones meteorológicas e hidrológicas que sean razonables en una cuenca de drenaje bajo estudio, FEMA(1998). Esta crecida está asociada a considerar como entrada la PMP en un modelo hidrológico de transformación precipitación-caudal.
Es importante señalar que el criterio de la CMP se aplica para el dimensionamiento de aliviaderos de embalses que cumplen ciertas condiciones de Ingeniería (volumen, altura del embalse, tipo de obras civil).
4. ASPECTOS HIDRÁULICOS ACTUALES EN EL DISEÑO DE ALIVIADEROS
En este parágrafo se presenta un análisis de la secuencia temporal de las teorías aplicadas en el diseño de aliviaderos en Argentina, desde principios del siglo XX hasta la actualidad, estudiando la utilización de dos modelos explicativos distintos, el primero determinístico y el segundo probabilístico.
La primera contribución argentina al diseño de evacuadores de crecidas se remonta a comienzos del siglo XX, con la propuesta de un nuevo perfil vertedor propuesto por el Ing. Julián Romero, que fuera utilizado muy posteriormente en diversas obras nacionales, por ejemplo en la presa El Carrizal, provincia de Mendoza.
Entre los problemas típicos clásicos que se plantean en el diseño de los aliviaderos, los más importantes están vinculados con la acción de la corriente aguas abajo del vertedero. Siendo necesario restituir al cauce fluvial los caudales erogados por el vertedero aparecen opciones diferentes para obras de gran altura (lanzamiento directo de la lámina líquida en salto de esquí, por ejemplo) y para obras de baja altura respecto a la carga, donde se requiere habitualmente un cuenco amortiguador de energía.
Cincuenta años después de las experiencias de Romero, los ingenieros José Gandolfo y Roberto Cotta desarrollaron un aporte original relacionado, ligado al estudio teórico-experimental de amortiguación de la energía cinética por medio hidrodinámico (Gandolfo y Cotta, 1955), presentando las expresiones de cálculo para dimensionar la estructura hidráulica.
Un tema muy importante es que, no sólo en la Argentina, sino a nivel mundial, todas las normas de diseño se basaban en la "hidráulica de los valores medios" sin tener en consideración los efectos de la alta turbulencia, en particular dentro de los cuencos amortiguadores a resalto hidráulico. La representación matemática de estos efectos está asociada con el estudio de valores extremos e implica la aplicación de un modelo probabilístico.
El diseño hidráulico convencional de disipadores a resalto, basado en valores medios temporales de velocidades y presiones ha sido tratado por numerosos investigadores y ha motivado prolongados estudios en diferentes laboratorios de hidráulica de diversos países. Como resultado de esas experiencias y datos de obras reales se poseen criterios definidos de diseño en manuales para ingenieros hidráulicos que cubren este aspecto para estructuras convencionales. A pesar de ello, no dejan de producirse problemas y destrucciones de cuencos amortiguadores de energía en todo el mundo.
En realidad, el flujo interno del resalto hidráulico es esencialmente de carácter no permanente, sometido a fluctuaciones macroturbulentas de presión, de carácter aleatorio, caracterizadas por grandes amplitudes y bajas frecuencias, y su comportamiento en ese sentido todavía no es completamente conocido. La naturaleza aleatoria de esas acciones fluctuantes hace necesario efectuar aproximaciones estadísticas para la obtención de resultados de aplicación práctica. Es que la disipación de energía en un resalto hidráulico está siempre asociada con severas fluctuaciones de presión que actúan sobre el piso y las paredes de los cuencos amortiguadores, así como sobre pilares, bloques y escalones que se encuentran en ellos.
Las acciones fluctuantes pueden ser responsables de importantes daños en estructuras hidráulicas causados por arrancamiento de losas, vibraciones estructurales, fatiga de materiales y cavitación intermitente debido a depresiones instantáneas, lo que hace indispensable la aplicación de la técnica de modelación física en escalas generosas.
Desde el punto de vista matemático, las fluctuaciones macroturbulentas en flujos reales pueden ser consideradas como un proceso estadístico con valores medios constantes (media y desvío estándar). A causa de su naturaleza aleatoria, la forma más adecuada de presentar una descripción cuantitativa del fenómeno es a través de funciones matemáticas que permiten obtener los parámetros estadísticos requeridos para los propósitos de diseño, como amplitud media cuadrática, amplitudes con diverso porcentaje de probabilidad de ocurrencia, asimetría de la función densidad de probabilidad, frecuencia dominante, etc. El pasaje de la hidráulica de los valores medios a la de valores instantáneos es un proceso razonablemente equivalente al pasaje de los cálculos clásicos de caudales de crecidas con los actuales modelos hidrológicos.
Los efectos destructivos de los fenómenos de pulsación macroturbulenta en disipadores a resalto hidráulico pueden ser constatados con numerosos ejemplos de accidentes ocurridos en obras de todo el mundo ( Lopardo, 1994). El Laboratorio de Hidráulica del Instituto Nacional del Agua ha desarrollado extensas investigaciones acerca de fluctuaciones de presión en flujo macroturbulento, contribuyendo sustancialmente a definir la influencia de las presiones fluctuantes en el diseño de disipadores a resalto ( Lopardo et al.,1987). Respecto de las investigaciones de carácter general, la utilización masiva de sensores adecuados, el decisivo aporte de la electrónica y el desarrollo de una técnica sencilla de análisis espectral y estadístico de señales aleatorias de baja frecuencia permitieron investigar en laboratorio los valores instantáneos de presión en escurrimientos macroturbulentos, como los que se producen en el interior de resaltos hidráulicos.
Así se evaluaron las amplitudes y frecuencias de fluctuación de presiones en resaltos libres, sumergidos y forzados. Se determinó así la influencia del número de Froude incidente, de la posición y de la relación de sumergencia sobre el coeficiente de presiones fluctuantes que vincula la amplitud de fluctuación a la energía cinética incidente. También se demostró que la presencia de elementos de disipación forzada (si bien aumentan la eficiencia de disipación) tiene como contrapartida un incremento de esas amplitudes de fluctuación de presiones y la concentración de energía alrededor de una frecuencia dominante.
A partir de los registros de presiones instantáneas, la función de densidad de probabilidad permite el cálculo de semiamplitudes positivas y negativas con diverso porcentaje de probabilidad de ocurrencia. En consecuencia, a partir del análisis estadístico resulta factible obtener la probabilidad de ocurrencia de semiamplitudes negativas de presión que puedan alcanzar la tensión de vapor del líquido (y llegar a la presión crítica de cavitación) de modo de transformarse en herramienta útil para verificar la tendencia a cavitación por pulsos de presión.
La cavitación por pulsos de presión puede producirse sin que estén presentes altas velocidades o depresiones medias muy pronunciadas. Por otra parte, para que se produzca la implosión de la burbuja no es necesario el desplazamiento de la cavidad hacia zonas de mayor presión, pues la variación de presión se produce en el mismo sitio. Además, la presencia de discontinuidades estructurales en el interior de flujos macroturbulentos (a veces provocadas para lograr una mayor eficiencia en cuanto a disipación de energía) también puede incrementar las amplitudes de fluctuación de presiones, la correlación espacial y la concentración de energía alrededor de una frecuencia dominante.
El uso de un parámetro estadístico basado en el desvío medio cuadrático de las amplitudes de fluctuaciones de presión derivado de una hipótesis Gaussiana, no resulta suficiente para alcanzar una correcta descripción del fenómeno de tendencia a la cavitación intermitente. Se cuenta con experiencias irrefutables que demuestran que las zonas donde se produce separación de la capa límite están asociadas con marcadas asimetrías negativas de la función de densidad de probabilidad de amplitudes. En consecuencia, aguas abajo de discontinuidades ubicadas en el interior del resalto (como pilares de vertedero, bloques de caída, dientes de choque o escalones) las semiamplitudes negativas de fluctuación son sustancialmente mayores que las derivadas de una aproximación Gaussiana.
De acuerdo con los registros de presiones fluctuantes y procesos de cavitación obtenidos de obras reales y en modelos físicos de laboratorio que cumplen exigentes condiciones de similitud se ha demostrado que el modelo probabilístico permite determinar valores medios de fluctuación muy ajustados a la realidad y tiende a exagerar las deflexiones extremas en el sentido de la asimetría, debido a la carencia del efecto compensador del aire incorporado. Como queda expuesto, el modelo físico es sumamente útil para verificar la tendencia a cavitación por pulsos de presión en estructuras sometidas a flujos turbulentos, aunque aparezcan ciertas anomalías en algunos parámetros en la comparación prototipo-modelo.
Se puede afirmar que la tendencia a la aparición de cavitación puede ser detectada a partir de los registros de presiones fluctuantes en modelo físico, recomendándose utilizar para tal fin la probabilidad de ocurrencia de amplitudes de presióndel 0.1%. Para un correcto diseño de un cuenco amortiguador de energía es necesario el conocimiento de las amplitudes de fluctuación de presiones, las correlaciones espaciales de las mismas y las variables de respuesta en frecuencia. Ello permitirá verificar la posibilidad de arrancamiento de losas, la acción de fatiga sobre los anclajes, la eventual presencia de vibraciones estructurales y la tendencia a la cavitación por pulsos de presión.
Para dar esos elementos al proyectista, se expresa la notable aptitud del modelo físicoconvencional sin distorsión, en escala suficientemente generosa como para evitar los efectos viscosos y capilares. En virtud de las verificaciones prototipo-modelo efectuadas en aliviaderos argentinos es posible asegurar que la similitud de flujos macroturbulentos en cuencos amortiguadores a resalto es adecuada cuando se aseguran condiciones de flujo que respeten las leyes de similitud desarrolladas para este caso particular.
5. CASO DE ANÁLISIS DE LOS RÍOS NEUQUÉN Y LIMAY
A continuación se presenta un caso de análisis que muestra los cambios en los modelos aplicados para estimación de los caudales máximos usados en el diseño de las obras realizadas en las cuencas de los ríos Limay y Neuquén.
Los primeros estudios en estas dos cuencas comenzaron en el año 1898 siendo el Ministerio de Obras Públicas de la Nación responsable de la construcción de canales de irrigación. En ese periodo el ingeniero italiano Cesar Cipolletti desarrolla el Estudio de Irrigación de los ríos Neuquén, Limay, Negro y Colorado. Luego, el ingeniero italiano Desio Severini proyecta los dos principales objetivos propuestos por el Ing. Cipolletti, un azud de derivación (dique Ballester) y un gran canal de derivación de las crecidas del río Neuquén hacia el Lago Pelegrini.
En la figura Nº 3 se presentan las crecidas observadas en el río Neuquén; las observaciones comienzan a principios del siglo XX (1903) y por ejemplo se pueden analizar los hidrogramas registrados en los años 1915 y 1916. En las crecidas en el río Neuquén se observa una fuerte pendiente de la curva de ascenso del hidrograma y los valores de los caudales máximos se alcanzan en pocos días. Esta característica está asociada con una importante diferencia con la cuenca del río Limay que es la carencia de lagos que actuen como embalses naturales regulando las crecidas que provienen de las precipitaciones en la Cordillera de los Andes y las características de aridez que presenta la cuenca.

Figura N° 3 Hidrogramas observados en el río Neuquén (Paso de los Indios).
La importancia de las cuencas y del desarrollo de nuevas obras hidráulicas para el control de crecidas, generación hidroeléctrica y riego se observan en la Tabla N° 3 donde se presentan los métodos de estimación de las crecidas para las obras construidas en esas cuencas.
Esta información permite otro análisis de la evolución de las teorías al identificarse dos obras hidráulicas cuyos parámetros de diseño fueron estimados con métodos estadísticos: el complejo El Chocón que tiene como objetivo controlar las crecidas del río Limay y Cerros Colorados sobre el río Neuquén, que controla las crecidas que afectaban el Alto Valle del Río Negro.

Tabla 3 Métodos de estimación de crecidas máximas aplicados en las cuencas de los ríos Limay y Neuquén (Fuente: Agua y Energía Eléctrica (1989).
En la siguiente figura Nº 4 se presentan las dos cuencas y las obras realizadas.
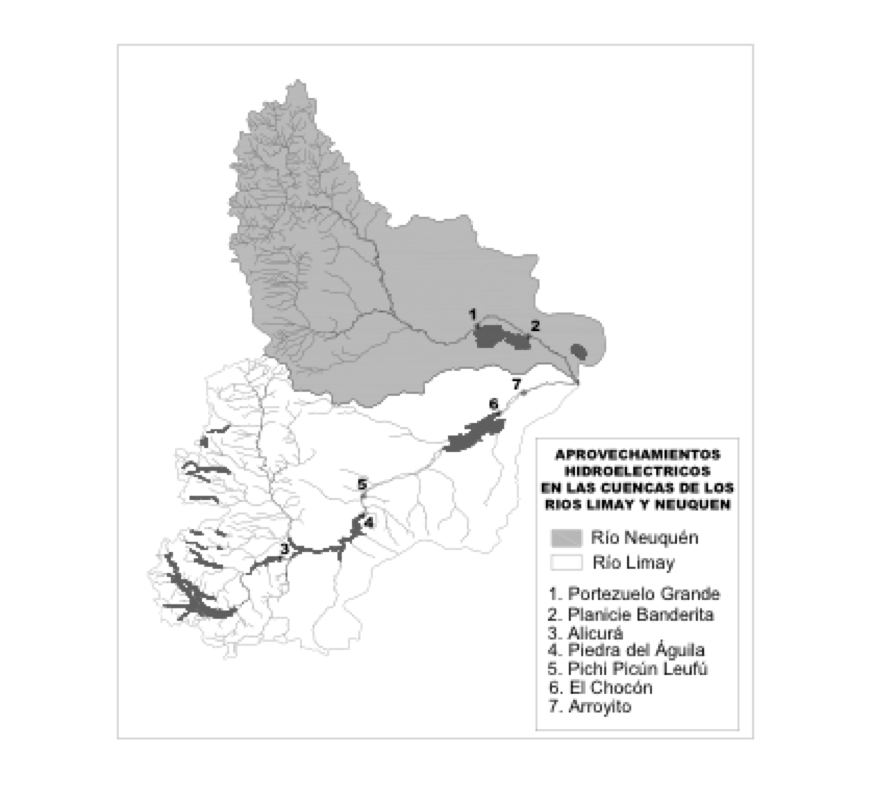
Figura Nº 4 Aprovechamientos hidroeléctricos y obra de control en los ríos Neuquén y Limay
La aplicación de los métodos estadísticos que se aplicaban a principios del siglo XX permitía estimar solamente la relación entre los caudales máximos de crecidas y el período de retorno y fueron usados en estudios desarrollados en las décadas de los años 60 y 70. A comienzos de la década de los ochenta estos métodos fueron reemplazados por una nueva forma de estimación de crecidas que incluye la combinación de la precipitación máxima probable y un modelo determinístico de transformación precipitación-caudal.
En resumen, durante la primera etapa de las obras construidas en estas dos cuencas, las estimaciones de las crecidas se realizaban con un modelo estadístico para definir la relación caudal máximo-período de retorno a partir de la serie observada de los caudales máximos. En la actualidad, se aplica un método de estimación de las crecidas de una mayor complejidad (CMP) y que incluye un modelo de transformación precipitación-caudal y utiliza la información hidrometeorológica observada en la cuenca.
Como un ejemplo de la primera etapa se puede señalar la aplicación de un método estadístico para la estimación de las crecidas que fueron utilizadas para el dimensionamiento de los embalses de El Chocón y de Cerros Colorados. En este caso se aplicó un modelo probabilístico que consiste en seleccionar una función de densidad de probabilidades adecuada a las observaciones de caudales máximos anuales, y luego estimar los parámetros del modelo y el caudal asociado a una probabilidad de ocurrencia del evento.
La función de densidad de probabilidades adoptada fue una Galton (Log-Normal) y se utilizaron los caudales máximos anuales observados en el río Limay en Paso Limay entre los años 1903 y 1958. La observación del histograma de frecuencia mostraba una fuerte concentración en el entorno de los caudales entre los 1600 y 2000 m3/s y también otro agrupamiento entre los 4600 y 5000 m3/s. Esta bi modalidad podría ser un consecuencia de la heterogeneidad del proceso de producción de crecidas las de origen pluvial y las de origen nival.
En la evolución de los modelos de valores extremos una importante contribución se debe al matemático Emil Gumbel que en 1941 presentó un modelo que aun se aplica en la actualidad. Desarrollos posteriores mostraron que ese modelo es un caso particular del modelo Generalizado de Valores Extremos (GEV) que actualmente se aplica para la estimación de los caudales máximos para obras hidráulicas menores.
Se presentan un ejemplo de los resultados de los valores estimados del modelo Gumbel con los obtenidos aplicando otros modelos de extremos para la misma serie observada en Paso Limay. En la Tabla N° 4 se observan valores más cercanos para el modelo Log-Normal II y más alejados con los modelos Pearson III y Log-Normal III. Un resultado interesante consiste en que las estimaciones realizadas con el modelo de Gumbel (también denominado EV1) y el GEV son cercanas.
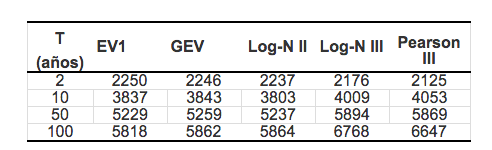
Tabla N° 4. Caudales máximos estimados en el río Limay para distintos periodosde retorno (Paso Limay).
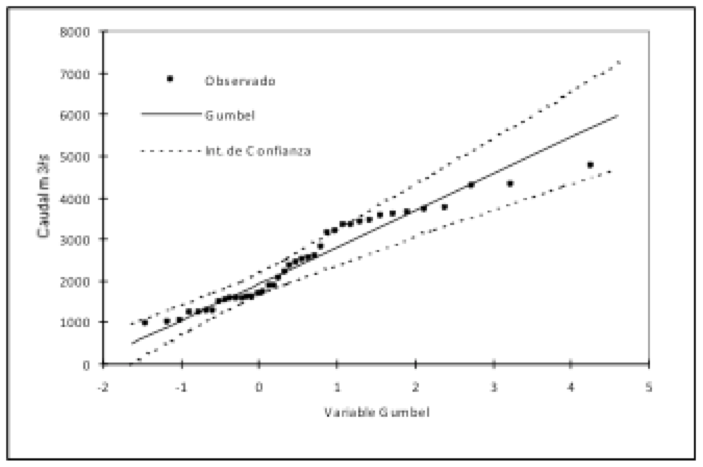
Figura N° 5 Ajuste del modelo Gumbel a la serie de caudales máximos diarios.
Como un ejemplo de la segunda etapa, durante la década de los 80 se realizó la estimación de la crecida máxima probable (CMP) para el aprovechamiento hidroeléctrico de Piedra del Águila, ubicado en la cuenca del río Limay, que fue construido por la empresa Hidroeléctrica Norpatagónica S. A. En la siguiente figura se presentan los hidrogramas en la estación Paso Limay cercana a la obra de Piedra del Águila.
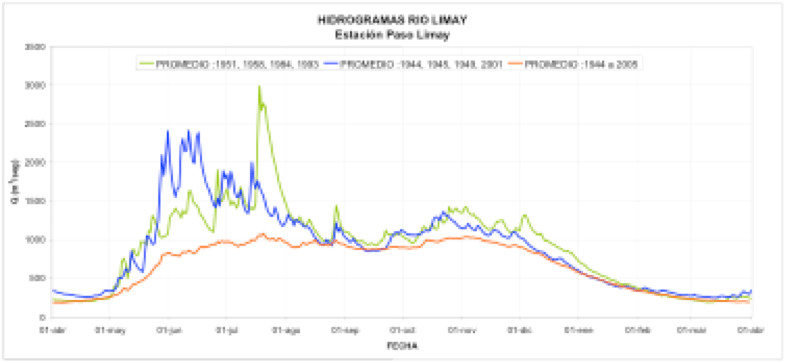
Figura N° 6 Hidrogramas observados en el río Limay (Paso Limay).
En este estudio se aplicó una nueva metodología que consistió en estimar la precipitación máxima probable (PMP), utilizar el hidrograma unitario, con parámetros estimados con el filtro de Kalman, para representar matemáticamente la transformación precipitación-caudal en las cuencas lacustres y en la cuenca intermedia se aplicó un modelo de simulación continua, el Streamflow Synthesis and Reservoir Regulation (SSARR); Devoto et al. (1982).
Otros antecedentes sobre las obras realizadas en el río Limay y el Neuquén. En el año de 1972/73 y para la obra de Alicura, Hidronor S.A. encargó un estudio de prefactibilidad de la crecida de diseño del aprovechamiento hidroeléctrico. Se aplicaron un modelo de hidrograma unitario (tipo Snyder) y una PMP maximizada por Hershfield. El caudal máximo estimado fue de 3000 m3/s. Este caudal finalmente fue el adoptado para el proyecto definitivo.
En el río Neuquén, en Paso de los Indios, la empresa Agua y Energía Eléctrica (AyEE) estimó la CMP en 18000 msup>3/s, se aplicó un hidrograma unitario adimensional y una PMP. Posteriormente, ·una consultora estimó la CMP en 14500 m3/s y luego de la ocurrencia de 10000 m3/s,durante la crecida de junio del año 2006, la AIC resolvió estimar la crecida incluyendo este nuevo evento y la nueva CMP se estimó en 25000 m3/s.
El Organismo de Regulación de Seguridad de Presas (ORSEP) comenzó, a fines del siglo XX, con la contratación de estudios para verificar la estimación de la crecida máxima probable de presas que se hallan dentro de su jurisdicción. La importancia de las revisiones que realiza ORSEP está sustentada en la necesidad de verificar las obras después de un tiempo de su construcción y en la significación que tiene utilizar la mayor cantidad de información hidro-meteorológica disponible a fin de incorporar nuevos eventos de crecidas observadas.
El Instituto Nacional del Agua verificó las CMP del aprovechamiento de Piedra del Águila utilizando un modelo determinístico del Cuerpo de Ingenieros de los Estados Unidos (HEC-1). Las cuencas lacustres fueron representadas con el modelo de Nash (1957) y la cuenca intermedia con otros modelos de transformación de la teoría del hidrograma unitario. A continuación se presenta un ejemplo de los resultados del modelo calibrado en Paso Limay.
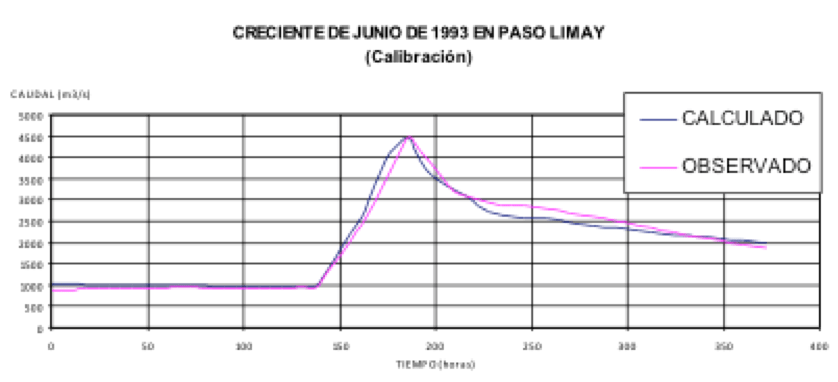
Figura N° 7 Contrastación de los resultados del modelo HEC-1 en el río Limay.
Desde un punto de vista hidráulico es interesante destacar los estudios desarrollados para las diversas obras de la cuenca del río Limay en cuanto a estos temas específicos. A pesar de ser una presa de gran altura, Alicura con más de 100 m de caída, tuvo que resignar una solución económica de lanzamiento directo de excedentes en forma de salto de esquí, tal como posee Piedra del Águila, debido a que la profundidad de erosión en la descarga ponía en riesgo la estabilidad de la la deraderecha frente a la obra de descarga. Esa profundidad máxima puede ser estimada mediante ecuaciones empíricas y determinísticas (Lopardo y Sly,1992) y verificadas en modelo físico.
La presa de Alicura consta de un disipador de energía a resalto de 36 m de ancho, 90 m de longitud y 24 m de altura, con sistemas de aireación forzada para evitar la cavitación en la rápida y anclajes de losas verificados mediante los análisis estadísticos de observaciones experimentales de modelos de laboratorio. Por otra parte, las roturas por cavitación por pulsos de presión en los bloques de disipación forzada del compensador de El Chocón en Arroyito impulsaron estudios de laboratorio que recomendaron la incorporación forzada de aire al cuenco amortiguador y consignas de operación uniforme de las compuertas de vertedero.

Fotografía Nº 1: Presa de Piedra del Águila (río Limay) con aliviadero en salto de esquí
El análisis de los conceptos anteriores permite señalar las siguientes conclusiones:
Los métodos más usados a principios del siglo XX se basaban en modelos de transformación precipitación-caudal muy simples y posteriormente en la aplicación de modelos de valores extremos a series de caudales máximos. Ambos modelos de estimación no permitían estimar el volumen de la crecida y solamente permitía determinar el caudal máximo.
Los métodos de estimación de la precipitación, variable de entrada a los modelos hidrológicos de precipitación-caudal, también han sufrido importantes cambios. El ejemplo clásico es la utilización de la precipitación máxima probable para la determinación de la crecida máxima probable en la estimación de caudales de diseño. Además, otra nueva fuente de incertidumbre en las estimaciones de los parámetros de diseño de las obras está asociada a los posibles efectos asociados con el cambio climático.
La utilización de modelos físicos ha permitido verificar y optimizar las estructuras de los aliviaderos, demostrando la necesidad de esa tecnología para definir obras seguras con la máxima economía.
Se ha demostrado en los aliviaderos de Alicura, Piedra del Águila y Arroyito la eficiencia del uso de aireación forzada para evitar los daños de cavitación en flujos de alta velocidad y en flujos de alta turbulencia.
5. CONCLUSIONES
En este trabajo se realizó un análisis metodológico de la evolución de la teoría hidrológica de transformación precipitación-caudal para demostrar la importancia de los cambios observados en las versiones de las técnicas de cálculo aplicadas en el diseño de obras hidráulicas. El principal objetivo fue relacionar los avances tecnológicos observados con la necesidad de realizar tareas de actualización de los estudios hidrológicos y de control de las obras hidráulicas construidas durante el siglo pasado en distintas cuencas de Argentina.
La mayoría de las obras hidráulicas argentinas, especialmente las de menor y mediano tamaño vinculadas al control de crecidas y derivación para riego, fueron construidas con anterioridad o durante el desarrollo de las teorías hidrológicas consideradas modernas que permiten evaluar con cierto grado de certeza una adecuada "crecida de diseño".
Durante las últimas décadas del siglo XX se han desarrollado nuevas teorías que permiten relacionar el proceso de ocurrencia de las crecidas y sus propiedades estadísticas con la geomorfología de la cuenca y su clima. Las nuevas investigaciones en Hidrología, que han utilizado la información de caudales extremos observados en distintos lugares del mundo, han demostrado la importancia de las características del clima para la variabilidad observada en las crecidas.
Estos nuevos estudios son importantes para nuestro país que presenta una distribución del recurso superficial con una marcada asimetría espacial. El 68% de la superficie de la Argentina presenta un clima árido o semiárido y en esas zonas se han realizado obras hidráulicas para mejorar el aprovechamiento del agua. Por lo tanto, se debería evaluar la importancia de la mayor variabilidad de los caudales debido al clima y la necesidad de estudiar la incertidumbre en las estimaciones de los caudales de diseño.
En resumen, el trabajo demuestra la importancia de avanzar en el desarrollo de estudios hidrológicos para las numerosas obras hidráulicas y para la investigación de las relaciones entre el clima y la ocurrencia de valores de caudales extremos. Los fundamentos de tipo técnico incluyen: el desarrollo de nuevas tecnologías que permiten realizar estimaciones más precisas, la necesidad de revisar las obras cuyos parámetros fueron determinados con modelos obsoletos y la importancia de incorporar los nuevos datos hidrológicos observados ante las evidencias de un posible impacto del cambio climático global sobre los caudales extremos.
Se recomienda que los aliviaderos cuyos estudios hidrológicos demuestren que estarán sometidos a crecidas más severas que las del diseño original, sean ensayados ante esa nueva situación mediante modelo físico, con las nuevas tecnologías desarrolladas para la medición de presiones y velocidades instantáneas.
La necesidad de adaptar los aliviaderos existentes para hacer frente a crecidas más exigentes en virtud de cálculos hidrológicos más precisos y los posibles efectos del cambio climático que podrían presentar tendencias a exagerar/incrementar los valores extremos, hace necesario tener en cuenta que no sólo debe preverse que la capacidad del aliviadero permita la erogación de estos caudales, evidentemente mayores, sino que las obras de disipación puedan hacer frente a esas nuevas condiciones sin daños que comprometan la seguridad total de las obras.
Ello requerirá sin dudas efectuar una nueva verificación experimental de las condiciones de funcionamiento de las estructuras sometidas a esfuerzos fluctuantes, cuyos valores extremos podrán ser modificados sensiblemente ante nuevas estimaciones de los caudales que deberán ser erogados por estructuras ya existentes.
6. BIBLIOGRAFÍA
Biswas, A.K. (1970) History of Hydrology. North-Holland Publishing Company.
Clark, C.O. Storage and the unit hydrograph. (1945) Amer. Soc. Civ. Engin. 110, 1416?1446.
Devoto,G., Manzano, R., Obertello, I., Seoane, R. (1982) Probable Maximum Flood for the design of Piedra del Águila Project. Comission International des Grands Barrages, San Francisco. 1543?1560.
(FEMA) Federal Emergency Management Agency Mitigation. (1998) Directorate Interagency Committee on Dam: Selection and Accommodation Inflow Design Floods for Dams.
Gandolfo, J.S., Cotta, R.D. (1955) Dissipateur d'energie, VI Congrès International de la IAHR, La Haya, Comunication C-23.
Gumbel, E.J. (1941) The return period of flood flows. Ann. Math. Stat, 12, 163-190.
Graham, W.J. (2000) Should Dams Be Modified for the Probable Maximum Flood?. Journal of the American Water Resources Association. 36, 953-963.
Hazen, A. (1930) Flood Flows: a Study of Frequencies and Magnitudes. Wiley, New York.
Hempel, C.G. (1988) La Explicación Científica. Editorial Paidos. Studio Básica. 1ª. Reimpresión, Madrid, España.
Lopardo, R., Sly E. (1992) Constatación de la profundidad máxima de erosión aguas debajo de aliviaderos en salto de esquí. Revista Latinoamericana de Hidráulica IAHR, Sao Paulo, Brasil, 4, 7-23.
Lopardo, R.A., De Lío, J.C., Vernet G.F. (1987) The role of pressure fluctuations in the design of hydraulic structures, Design of Hydraulic Structures, editado por R. Kia y M.L. Albertson, Colorado State University, Fort Collins, 161-175.
Lopardo, R.A. (1994) Solicitaciones dinámicas en disipadores a resalto. Anales de la Academia Nacional de Ciencias Exactas, Físicas y Naturales, Buenos Aires. 46, 95-100.
Meigh, J.R., Farquharson, F.A, Sutcliffe, J.V. (1997) A worldwide comparison of regional flood estimation methods and climate. Hydrological Sciences Journal, 42, 225-244.
Moyano, C., Díaz, R. (2006) Tierras secas en Argentina. Anales de la Asociación de Agrometeorología Argentina (AADA).
Nash, J.E. (1957) The form of the instantaneous unit hydrograph. International Association for Scientific Hydrology. Toronto, III, 114-121.
Nash, J.E. (1960) A unit hydrographic study with particular reference to British catchments. Proc. Institution of Civil Engineers. 17, 249?282.
Rodríguez?Iturbe, I., Valdés, J.B. (1979) The geomorphologic structure of hydrologic response. Water Resources Research. 15, 1409?1420.
Rodríguez?Iturbe, I., Devoto, G.A., Valdés, J.B. (1979) Discharge response analysis and hydrologic similarity: the interrelation between the geomorphologic IUH and the storm characteristics. Water Resources Research. 15, 1435?1444.
Rodríguez?Iturbe, I., Gonzalez?Sanabria, M., Bras, R. (1982) A geomorphoclimatic theory of the Instantaneous Unit Hydrograph. Water Resources Research. 18, 877?886.
Rosso, R., Nash, A. (1984) A model relation to Horton orden ratios. Water Resources Research. 20,914?920.
Sherman, L. K. (1932) Streamflow from rainfall by the Unit-graph Method. Eng. News Records 108, 501-505.
Seoane, R. Moretti A. (1999) Programas de investigación en Hidrología: La teoría del hidrograma unitario. Ciencia e Investigación. Tomo 52, 61-68.
Snyder, F.F. (1938) Synthetic unit-graphs. Trans. Am. Geophys. Union, 19, 447-454.
Valdés, J.B., Fiallo, Y., Rodríguez?Iturbe, I. (1979) A rainfall?runoff analysis of the geomorphologic IUH. Water Resources Research. 15, 1421?1434.
Ven Te Chow. Handbook of Applied Hydrology. McGraw-Hill. 1964.
Vornetti, A., Seoane R. (2004) Desarrollo de una nueva función de densidad de probabilidades del caudal máximo y su aplicación en dos cuencas (Argentina). XXI Congreso Latinoamericano de Hidráulica. ·São Pedro, Brasil.
Vornetti, A., Seoane R. (2005) A new derived flood frequency distribution and analysis of the watershed response model. Simposia - Model evaluation and comparison: uncertainty analysis and diagnostics. VII International Association of Hydrological Sciences. Scientific Assembly. Brasil.
·Wilson, B.N., Brown, J.W. (1992) Development and evaluation of a dimensionless unit hydrograph. Water Resources Bulletin American Water Resources Association. 28, 397-408.
WMO Manual for the Estimation of Probable Maximum Precipitation. (1986) World Meteorological Organization Nº332. Operational Hydrology Report 1.

