LA NATURALEZA PUEDE EXPLICAR EL ENIGMA DEL ASTEROIDE QUE PARECE UNA NAVE ESPACIAL
9 agosto, 2019IDENTIFICAN UNA POSIBLE DIANA TERAPÉUTICA PARA LA ENFERMEDAD DE KENNEDY Y EL CÁNCER DE PRÓSTATA
12 agosto, 2019Secciones:
Novedades
Julio comenzó y terminó con una muestra colectiva de innumeracy, un concepto análogo al de iletrado o analfabeto pero respecto a las matemáticas: los telares, mandalas, fractales, flores... de la abundancia, prosperidad, gratitud, solidaridad, nueva economía... entre muchas otras versiones.La matemática involucrada aquí es clásica, elemental: progresiones geométricas como el cuento de la anciana que va al mercado con siete bolsas, en cada bolsa hay siete gatos... que se encuentra en el Liber Abaci de Fibonacci, del año 1202, pero es una historia tan antigua que una de sus versiones aparece en tabletas babilónicas de hace 3800 años, y otra estaba en el Papiro Ahmes, egipcio, de la misma época.
El nombre popular de estos mecanismos es el de esquema de Ponzi, o también estafa piramidal: si cada participante convence a otros k de participar, el número de involucrados crece rápidamente. Para k=8, en solo siete pasos superamos la población Argentina, lo cual muestra que no puede funcionar.
Muchos de los participantes argumentan que no, que nada impide a alguien participar más de una vez, así que no ven una contradición. Otro argumento -me parece- es más efectivo: si todos ponen 1 peso y todos ganan 8, ¿de dónde salen los 7 de diferencia?
Un paper del arXiv
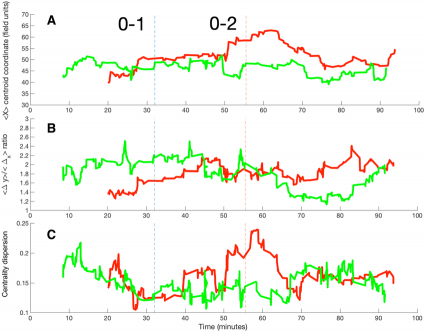
Dos, para ser exactos. Pero sólo porque ambos incluyen mapas y entra la Argentina en ambos estudios, así que no me podía decidir.El primero: The demography of the peripatetic researcher: Evidence on highly mobile scholars from the Web of Science, de Samin Aref, Emilio Zagheni, y Jevin West (en Lecture Notes in CS, Proc. 11th Int. Conf. on Social Informatics, Doha, Qatar, 2019). El trabajo analiza a los académicos que han publicado con afiliaciones en al menos tres países distintos entre 1956 y 2016. Consideran como país de origen al de su primera publicación, y la edad académica la cuentan entre la primera y la última publicación. La distribución por edades está en el siguiente gráfico:

Para analizar la fracción de peripatéticos que regresa a su país de origen consideran tres grupos de edades: hasta 7 años, más de 7, y el resto. Por ejemplo, esta es para 1-7:

¿Qué imaginan que ocurre en los de 7 a 14? La respuesta, en el paper!
Por último, consideran la red de viajes de estos científicos según el país de origen, para distintos países.

El segundo: Historical comparison of gender inequality in scientific careers across countries and disciplines, de Junming Huang, Alexander J. Gates, Roberta Sinatra, y Albert-Laszlo Barabasi.
Este trata un tema de gran actualidad, el gender gap en la trayectoria académica de hombres y mujeres, medido en términos de sus publicaciones y sus citas. l.

No digo mucho más, porque hay tantas cosas para mirar en lo que midieron, que creo que cada uno elegiría distintos puntos donde enfocar. Por ejemplo, y sólo porque el gráfico es muy lindo, el gap en la duración de la carrera está muy correlacionado con el gap en productividad (aunque el gap en la duración es mayor que el gap de las edades jubilatorias, hasta donde se puede ver).
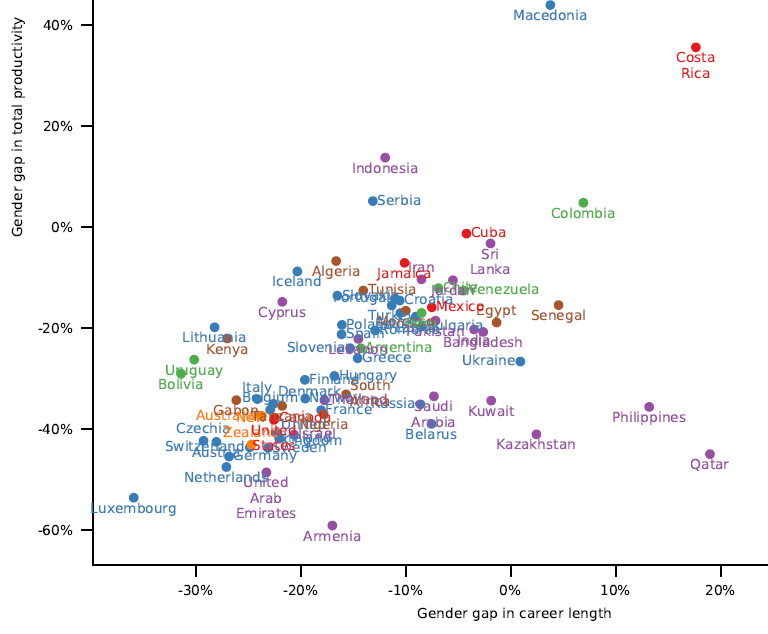
El trabajo tiene un punto que no me gusta: trabajan con más de 3 millones de científicos cuyo género fue identificado automáticamente, a partir de una base de poco menos de 8 millones. Los porcentajes pueden variar muchísimo si hay un sesgo en ese grupo que no se identifica. Sería interesante chequear con una fracción random de estos, identificándolos, para ver si los porcentajes se mantienen.
En un rincón de la red
Visto en Facebook

De la gente de BadScienceJokes, con el título: Ninguna persona racional haría esto.
Yo seguro que no lo hubiera hecho, olvidarse de pintar una coma después del 3 es imperdonable.
Solo en twitter + un blog
En @Math4Everybody encontramos:
El tweet recomienda un post del blog Mathematics, Learning and Technology, donde pueden encontrar colecciones de posters con más problemas, teoremas, curiosidades, etc.
Youtube
Los milennials siguen a un montón de youtubers centennials, y existen canales de toda clase. Por ejemplo, uno de los más interesantes es el de Ter, una arquitecta española que estudió en la Politécnica de Madrid.
Sin más, los dejo con su propia presentación del siguiente video: "si quieres saber lo que es la homotecia, la perspectiva caballera, militar y egipcia, la simetría axial y central, la isométrica, dimétrica y trimétrica y la perspectiva cónica, lo que tienes que hacer no es leerte a Euclides ni usar escuadras, sino estudiar detenidamente los emojis de whatsapp."
Un problem(it)a
5.- Digitos al azar: repartimos los números del 1 al 9 al azar en una grilla de 3x3. ¿Cuál es la probabilidad de que las sumas de los dígitos de cada una de las filas y en cada una de las columnas sea siempre impar?
¿Y si reparto los números del 0 al 8?
Soluciones del mes anterior
3.- Mentalmente: escribamos un número entero de N dígitos que son todos cincos, 5....5, hagamos 1/5....5, y calculemos -son grados, no radianes- el seno de la 1/5....5. ¿Cuánto da?Solución: el 5...5 (N dígitos, todos 5) es la parte entera de 10^N * 5/9, con lo cual, tras cambiar de grados a radianes, usamos que sen(x) es aproximadamente x para x chico:

4.- Esfera: me ofrecen una esfera de oro, de 1 metro de radio, o su cáscara -también de oro- de 1 cm. de diámetro. ¿Cuál debería elegir si vivo en dimensión 100?
Solución: la pueden leer aquí, era un problema para ingresar al doctorado. Se puede resolver con facilidad usando proporcionalidad, cualquier cuerpo cambia su volumen por un factor r^N si se lo dilata por un factor r estando en dimensión N, no sólo para una esfera.
Así, el volumen de la cáscara es proporcional a 1,01^N - 1^N (una esfera de radio 1,01 menos una esfera interior de radio 1), mientras que el de la esfera es proporcional a 1^N. En definitiva, si 1,01^N > 2, nos conviene la cáscara. Con la calculadora y N=100 sale, pero también podemos hacer Taylor, 1,01^N es aproximadamente 1 + 0,01 * N + 0,01^2*N*(N-1)/2, y ya está.
¿Soluciones? ¿Otras soluciones? ¿Variantes? ¿Errores? ¿Comentarios? ¿Preguntas? Me encuentran en jpinasco@gmail.com.
Secciones:
- Novedades –
- Un paper del arXiv –
- En un rincón de la red –
- Problem(it)a –